A large number of high-average-power (HAP) petawatt-class lasers are in early development stages around the world. In comparison to existing petawatt lasers that operate at low repetition rates (typically below 1 Hz), these new HAP lasers are expected to deliver pulse energies > 1 Joule at repetition rates > 1 kHz, producing average powers up to 100’s of kW. Many of these will operate with pulse durations below 10’s of fs, thus requiring spectral bandwidths of up to 100 nm or higher. These combined requirements exceed what is possible with the current state-of-the-art in pulse-compression diffraction grating technology. In this paper we consider limitations and trade-offs associated with gold gratings (used in most existing petawatt lasers) and multilayer dielectric (MLD) gratings.
Thermal expansion of gratings caused by absorbed heat from a HAP laser beam causes wavefront deformation, which not only impedes the ability to focus the beam on target, but also degrades the pulse temporal characteristics. For existing petawatt lasers gold gratings are ideal due to their broad spectral and angular bandwidths, resulting in optimal compressor designs for 10’s of fs pulses using moderate dispersion (~ 1480 lines/mm) gratings. However, these gratings can absorb up to several % of the incident light. MLD gratings appear to be an obvious alternative for HAP lasers due to their extremely low absorption. Yet the sensitive role optical interference plays in these gratings leads to a limited range of dispersion values that yield broad spectral and angular bandwidth solutions for a given wavelength. For the desired more moderate dispersion values, MLD gratings must be operated at the Littrow angle, requiring compromises in compressor design. Below we show examples illustrating these trade-offs.
Consider a Ti:Sapphire laser system with an 800 nm center wavelength and a pulse width of about 30 fs (FWHM), and suppose this pulse has been stretched to 1 ns for chirped-pulse amplification (CPA). The FWHM of the pulse spectrum is then about 0.0015 (800 nm)2 / 30 fs = 32 nm. To keep things simple, we assume a 4-grating compressor, though many compressors are designed with two gratings and a mirror periscope. The compressor may be designed for high-angle incidence, as shown in Fig. 1(a), or low-angle incidence, as shown in Fig. 1(b).
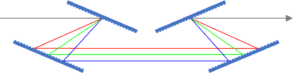
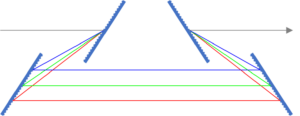
The high-angle incidence design exhibits lower overall temporal dispersion for a given grating frequency and separation, and has the advantage that the intensity on the final grating—where the instantaneous peak power is highest—is lower due to a larger projected angle of the beam on the grating, thus resulting in a potentially higher pulse energy before laser damage occurs. The low-angle incidence design exhibits higher dispersion for a given separation between the gratings, and therefore can have compressor geometry advantages for some systems.
An ideal grating frequency for this system is 1480 lines/mm, which has a Littrow angle at 800 nm of 36.3º. A typical total angular deviation for a high-angle incidence compressor is about 30º, which corresponds to a 52.8º angle of incidence (AOI) and a 22.8º angle of diffraction (AOD). For this combination of angles each pair of gratings provides 7.5 ps/nm of temporal dispersion per meter of separation between the gratings, so there is 14.9 ps/nm of dispersion per meter of separation for the full compressor. Here it is assumed the separation between two parallel gratings is measured along the direction normal to the grating surfaces. If the pulse is stretched to 1 ns, the distance between the gratings in each pair should be 2.1 m measured along the normal direction, or 2.3 m measured along the path taken by a ray of light at 800 nm.
The theoretical diffraction efficiency (DE) as a function of wavelength and angle of incidence is shown in Fig. 2 for a typical gold reflection grating. This calculation assumes the light is p-polarized; i.e., the electric field vector is parallel to the plane of incidence and perpendicular to the grating lines.
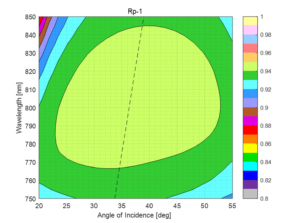
Note that the DE is between 90 and 95%, and is very uniform over both wavelength and angle. Even for a perfect gold grating there will always be at least several % of loss due to absorption in the gold. It is this absorption that leads to heating problems.
Next consider a compressor configuration based on the same gratings, but with higher dispersion and smaller total deviation angle. Suppose the light is incident on the first grating at an AOI = 31.5º, corresponding to an AOD = 41.5º, for a total deviation of 10º. In this case each pair of gratings provides temporal dispersion of 13.9 ps/nm per meter of separation, so there is 27.8 ps/nm per meter for the full compressor. For a 1 ns stretched pulse, the distance between gratings in each pair should be 1.2 m measured along the normal direction, or 1.5 m measured along the path taken by a ray of light at 800 nm.
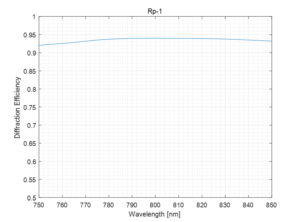
The theoretical DE vs. wavelength at 31.5º is shown in Fig. 3. It is very similar to that of the higher angle case.
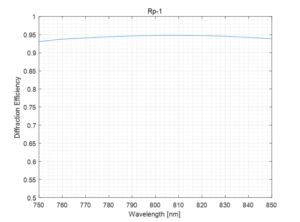
To avoid heating that can occur in gold gratings in higher-average-power lasers, the most obvious alternative is a multilayer dielectric (MLD) reflection grating. These are known to exhibit the highest diffraction efficiency of all pulse compression gratings, with extremely low loss. Almost all of the light that is not diffracted into the desired –1 order is reflected (0th order diffraction).
Consider a one-for-one replacement for the gold grating example above — an MLD grating with 1480 lines/mm. The theoretical DE as a function of wavelength and angle of incidence is shown in Fig. 4 for an optimized MLD reflection grating. The grating has been designed to achieve high DE over as broad of a spectral and angular bandwidth as possible, using a manufacturable grating profile and materials known to achieve high laser-induced damage threshold (LIDT) performance. In this case the light is s-polarized; i.e., the electric field vector is perpendicular to the plane of incidence and parallel to the grating lines.
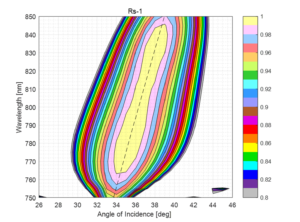
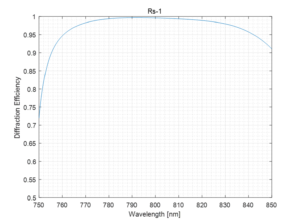
Notice that the DE for the MLD grating is substantially higher than that of the gold grating at wavelengths close to the Littrow angle. However, in contrast to the gold grating, the DE drops off rapidly as the angle moves away from Littrow. As a result it is not straightforward to achieve a total deviation angle larger than a few degrees. Even for relatively large grating separations of 1 to 2 meters, as considered in the examples above, an angular deviation of only a few degrees severely limits the beam size possible in such a compressor.
An alternative to working with a very small angular deviation is to operate the grating at the Littrow angle as projected onto the plane of incidence (the plane normal to both the grating surface and the grating lines), but at an angle slightly off this plane. This configuration is referred to as out-of-plane (OOP). The DE performance for a similar grating to the one shown in Fig. 4 is shown in Fig. 5 for operation at 5º OOP. From a compressor design standpoint, this configuration is equivalent to a total angle deviation of 10º.
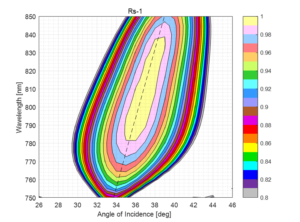
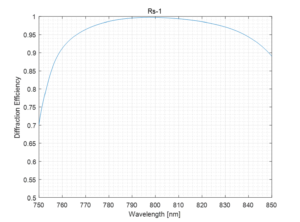
The DE at 800 nm is just as high as the in-plane case, but it drops off a little more rapidly for wavelengths away from 800 nm. For example, the 95% DE bandwidth exceeds 80 nm for the case of true Littrow incidence (see Fig. 4, right), but drops to about 70 nm for the 5º OOP case (see Fig. 5, right).
Because a 1480 lines/mm MLD grating may be operated only at or near the Littrow angle, the dispersion will also be different from the gold grating examples described above. At the Littrow angle of 36.3º, the temporal dispersion for a 4-grating compressor is 22.3 ps/nm per meter of grating separation. For a 1 ns stretched pulse, the distance between gratings in each pair should be 1.4 m measured along the normal direction, or 1.8 m measured along the path taken by a ray of light at 800 nm.
The first example of a gold grating above represents a common compressor configuration, in which the total dispersion is 14.9 ps/nm per meter. However, a 1480 lines/mm MLD grating operated at the Littrow angle necessarily yields higher dispersion. This difference was compensated above by using a smaller grating separation (1.4 m vs. 2.1 m, as measured along the normal direction). But what if the beam size does not allow a shorter compressor configuration? One might try to use a lower-dispersion MLD grating. For example, a 1310 lines/mm grating operated near the Littrow angle at 800 nm of 31.6º yields dispersion from a 4-grating compressor of 14.8 ps/nm per meter, which is about the same as that from a 1480 lines/mm grating with a 52.8º AOI. If this grating were operated in the OOP configuration, a larger grating separation could be used than that of the 1480 lines/mm MLD.
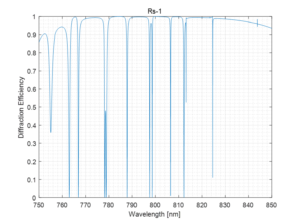
While this approach might seem reasonable, the decrease of DE away from the Littrow angle is not the only problem that occurs with lower-dispersion MLD gratings. Consider the DE performance of the 1310 lines/mm grating shown in Fig. 6. A number of sharp resonance dips emerge. These are called Guided-mode Resonances (GMRs), and they result from diffraction orders coupling light into (and out of) the higher-index MLD thin-film layers which act like planar waveguides. Here the GMRs result from the –2 and +1 diffraction orders (which are nonpropagating outside the substrate) coupling to the MLD layers.
Clearly these GMRs present a problem. Even if one could live with the loss of efficiency from these fairly narrow resonances, they cause substantial enhancement of the electric fields inside the MLD layers and can lead to appreciable degradation of the LIDT. In some cases careful design of the MLD structure can mitigate the resonance dips, but for this particular case (1310 lines/mm grating at 800 nm) they cannot be eliminated completely. As the grating dispersion is decreased further (below about 1100 lines/mm), GMRs associated with the –2 and + 1 orders no longer interfere with the 800 nm region, so it is possible to make an MLD grating with substantially lower dispersion if the system requires it.
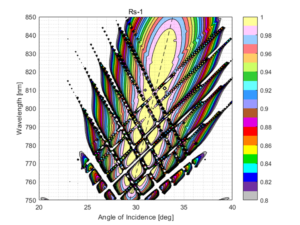
Those familiar with MLD gratings might wonder why the angular bandwidths shown above are so narrow. Indeed MLD gratings with frequencies around 1740 lines/mm are commonly used in 1054 nm laser systems with quite large total angular deviations. It turns out that for a certain combination of the wavelength and grating frequency, which corresponds to a Littrow angle near 65º, MLD gratings can exhibit such broad angular bandwidths. This behavior has to do with the role of interference in MLD gratings.
MLD gratings are much like a Mach Zehnder interferometer, where the two beamsplitters are replaced by the transmission grating on top (through which the light passes twice), the two beam paths are the 0th and the –1st order diffracted beams, and the mirrors are replaced by the MLD reflector below the grating. Just the right accumulation of relative phase upon diffraction, propagation, and thin-film reflection is required to achieve all light in the –1st order of reflection. This requirement can be met over a broad range of angles for a certain ratio of wavelength to grating period, which corresponds to a Littrow angle of about 65º. For almost all other cases, however, MLD gratings tend to provide high diffraction efficiency only very close to the Littrow angle.
As an example of a broad angular bandwidth grating, the theoretical DE as a function of the wavelength and angle of incidence is shown in Fig. 7 for an optimized 2290 lines/mm MLD reflection grating. At 800 nm the Littrow angle for this grating is 66.3º. It has been designed to achieve high DE over as broad of a spectral and angular bandwidth as possible, using a manufacturable grating profile and materials known to achieve high LIDT performance. The light is s-polarized. For an AOI of 75º the AOD at 800 nm is 60º, yielding a total angular deviation of 15º.
The DE at 800 nm is extremely high, but it drops off more rapidly for wavelengths away from 800 nm than the 1480 lines/mm MLD grating shown above. For example, the 95% (theoretical) DE bandwidth is just under 50 nm, compared to 70 nm for the 1480 lines/mm grating at Littrow incidence and 5º OOP (see Fig. 5, right).
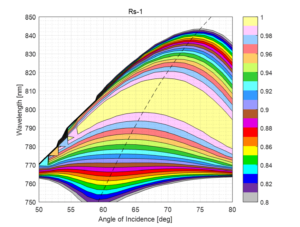
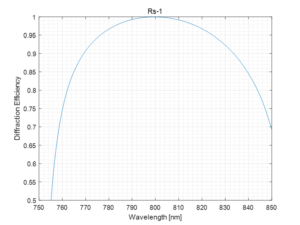
This design is viable from a DE perspective, though the spectral bandwidth is not as broad as that for the lower-dispersion gratings. However, the dispersion is very high. The temporal dispersion for a 4-grating compressor at an AOI of 75º is 224 ps/nm per meter of grating separation. To compress a 1 ns stretched pulse, the gratings would have to be separated by only 142 mm, which results in a significantly reduced maximum beam size compared to the lower-dispersion grating geometries described above.
Conclusion:
For ultrashort-pulse (10’s of fs) CPA Ti:Sapphire laser systems operating around 800 nm, 1480 lines/mm gold pulse compression gratings offer a nearly ideal solution in terms of the spectral performance of the diffraction efficiency. However, because these gratings absorb several % of the incident light, they are not ideal for high-average-power lasers.
MLD gratings offer the highest diffraction efficiency and can offer a viable alternative for some systems, but they have certain limitations. MLD gratings with comparable dispersion have a spectral bandwidth limited to about 100 nm, and a much narrower angular bandwidth. These gratings must be operated at or near the Littrow angle, thus require operation out-of-plane for a total angular deviation greater than a few degrees. MLD gratings with lower dispersion can exhibit problematic spectral features called Guided-mode Resonances (GMRs), though for much lower dispersions (below about 1100 lines/mm) these can be avoided. MLD gratings can also exhibit fairly broad angular bandwidths, but only for very high dispersion gratings, and these tend to have somewhat lower spectral bandwidths.
The best solution for very short pulse, high-average-power systems could be actively cooled gold (or even hybrid metal-dielectric) gratings. These are in the early stages of exploration today.
5 Commerce Way, Carver, MA 02330, USA|+1.508.503.1719|sales@plymouthgrating.com